Точка Лемуана треугольника.

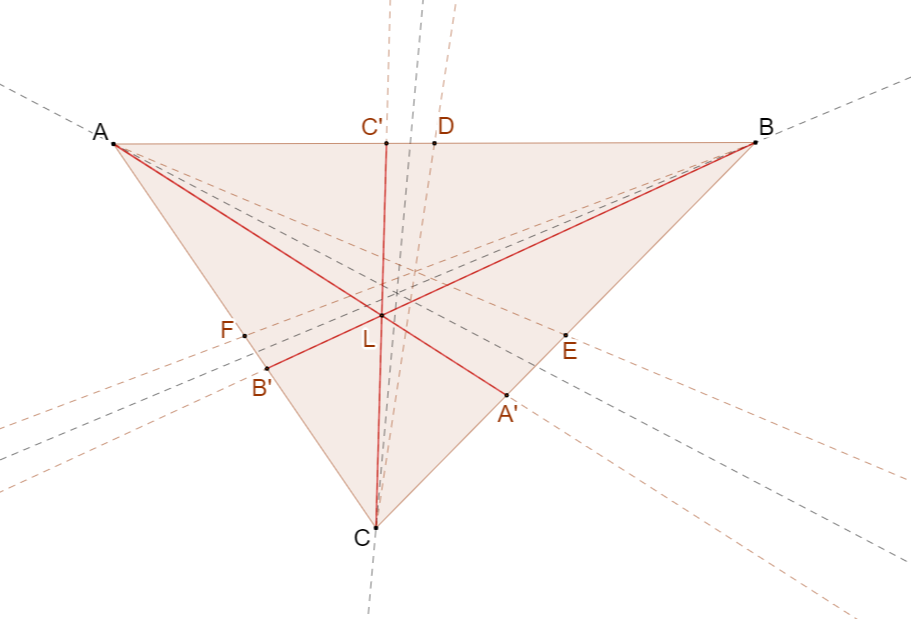
Симедиана треугольника — чевиана треугольника, симметричная медиане треугольника относительно биссектрисы угла, проведенной из того же угла, что и медиана данного треугольника.

На рисунке CC’, BB’ и AA’ — симедианы треугольника. Они симметричны медианам СD, BF и AE относительно биссектрис углов соответственно.

Основное свойство симедианы треугольника:

Отрезки, на которые симедиана делит противоположную сторону, пропорциональны квадратам прилежащих сторон.

Точка Лемуана — точка пересечения симедиан треугольника.

Свойства:

1. Точка Лемуана является центроидом треугольника, образованного её проекциями на стороны исходного треугольника;
2. Расстояния от точки Лемуана до сторон треугольника пропорциональны длинам сторон;
3. Сумма квадратов расстояний от точки Лемуана до сторон треугольника минимальна.