Векторы и координаты на плоскости.

Координата точки — это место точки на плоскости. Она задается двумя числами — абсциссой и ординатой. Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения перпендикуляра с осью Ox называется абсциссой точки, а точка пересечения с осью Oy — ординатой точки.

Обозначение: $M(x;y)$ , где $x$ — абсцисса точки, а $y$ — ордината точки.

Отрезок на плоскости задается двумя точками (концами отрезка). Длину отрезка с концами в точках с координатами $(x_{1};y_{1})$ и $(x_{2};y_{2})$ можно найти по формуле:

$d=\sqrt{(x_2-x_1)^{2}+(y_{2}-y_{1})^{2}}}}}$

Координату середины отрезка можно найти по следующей формуле:

$M(x;y)=\left (\frac{x_{1}+x_{2}}{2};\frac{y_{1}+y_{2}}{2}\right )$

Координату точки, делящей отрезок в отношении $m:n=\lambda$ , можно найти по следующим формулам:

$N(x;y)=\left ( \frac{n \cdot x_{1}+m \cdot \ x_2}{n+m};\frac{n \cdot y_{1}+m \cdot y_{2}} {n+m} \right )$

$N(x;y)=\left ( \frac{x_{1}+\lambda \cdot \ x_2}{1+\lambda};\frac{y_{1}+\lambda \cdot y_{2}} {1+\lambda} \right )$

Вектор — направленный отрезок. Графически, начало вектора обозначается точкой, а конец — стрелкой. Вектор на плоскости с началом в точке с координатой $(x_{1};y_{1})$ и концом в точке с координатой $(x_{2};y_{2})$ имеет координату: $(x_{2}-x_{1};y_{2}-y_{1})$ .

Нулевым вектором называется вектор, у которого начало и конец совпадают.

Длиной или модулем вектора называется неотрицательное число, равное длине отрезка, который задает вектор. Длина нулевого вектора равна нулю.

Длина вектора с координатой $(x;y)$ равна:

$d=\sqrt{x^{2}+y^{2}}}}}$

Два вектора на плоскости называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. В противном случае векторы называются неколлинеарными.

Два коллинеарных вектора называются сонаправленными, если их направление совпадает.

Два коллинеарных вектора называются противоположно направленными, если их направление не совпадает.

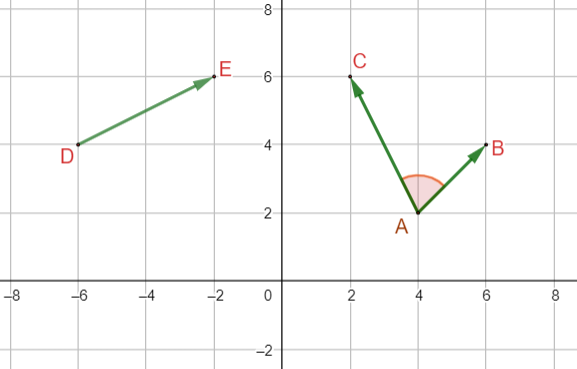
Скалярное произведение — это операция над двумя векторами, результатом которой является число.

Скалярное произведение двух векторов можно вычислить по следующим формулам:

$(\vec{a}(x_{1};y_{1});\vec{b}(x_{2};y_{2}))=x_{1} \cdot x_{2}+y_{1} \cdot y_{2}$

$(\vec{a}(x_{1};y_{1});\vec{b}(x_{2};y_{2}))=\sqrt{(x_2-x_1)^{2}+(y_{2}-y_{1})^{2}}}}} \cdot \cos \alpha$

, где $\alpha$ — угол между векторами.

Следовательно, угол между векторами можно вычислить зная их скалярное произведение и длину:

$\cos \alpha=\frac {(\vec{a}(x_{1};y_{1});\vec{b}(x_{2};y_{2}))} {\sqrt{(x_2-x_1)^{2}+(y_{2}-y_{1})^{2}}}}}}$