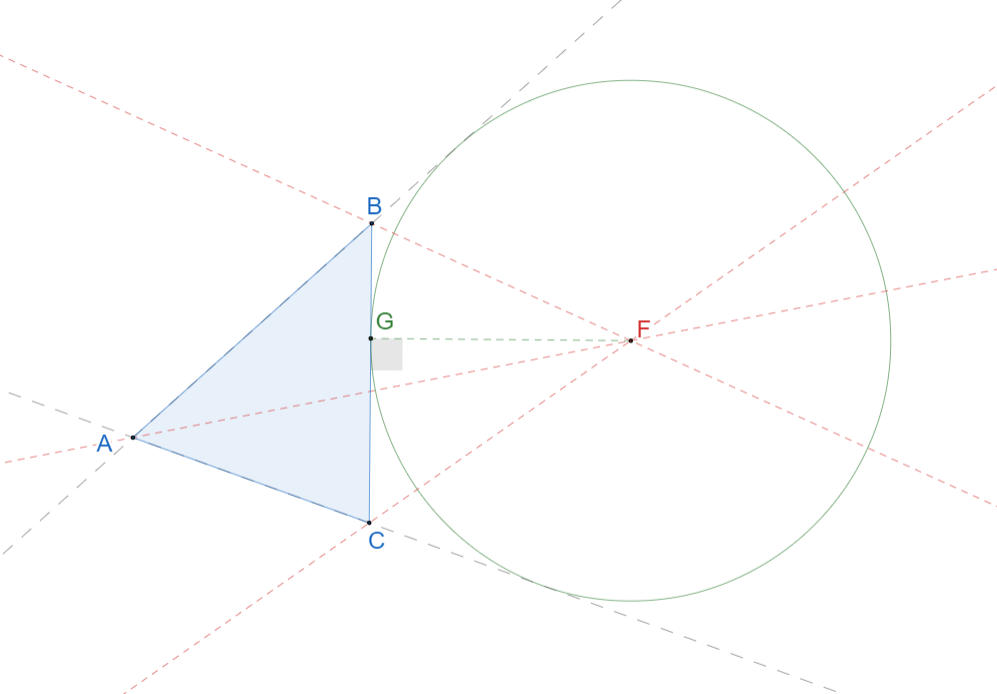
Определение.
Окружность, касающаяся стороны треугольника и продолжения двух других его сторон, называется вневписанной окружностью треугольника.
Теорема 1.
Центр окружности, вневписанной в треугольник, есть точка пересечения биссектрис двух внешних и одного внутреннего угла треугольника.

Доказательство.
BF — биссектриса ∠JBG, следовательно F равноудалена от сторон данного угла.
СF — биссектриса ∠JСH, следовательно F равноудалена от сторон данного угла.
Следовательно, точка F равноудалена от сторон ∠BAC.
Таким образом, точка F — центр окружности, касающейся стороны BC и продолжения сторон AB и AC. По определению данная окружность называется вневписанной окружностью треугольника.
Теорема 2.
Отрезок, соединяющий вершину треугольника с точкой касания вневписанной окружности и противолежащей стороны, делит треугольник на два треугольника равного периметра.

Доказательство.
BJ=BG, GC=CH и AJ=AH (свойство отрезков касательных, проведенных из одной точки к окружности).
PΔABC=AB+BC+AC=AB+BG+GC+AC=AB+BJ+AC+CH=AJ+AH.
Так как AJ=AH, то PΔABC/2=AJ=AH и PΔABC/2+AG=AJ+AG=AH+AG=AB+BG+GA=AC+CG+GA.
Следовательно, отрезок AG поделил треугольник ABC на два треугольника равного периметра PΔABC/2+AG.
Советую прочитать: